Electromagnetism Explained: Key Theories, Equations, and Practical Uses

ELECTROMAGNETISM

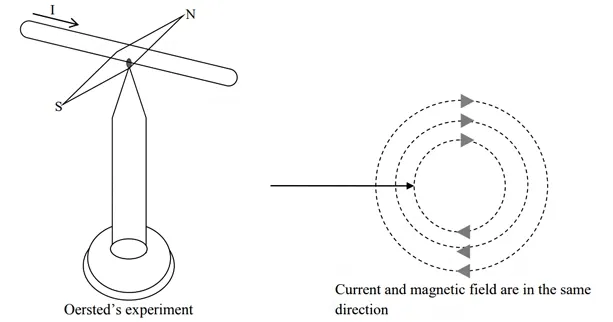
When a conductor carries an electric current, a magnetic field is produced around that conductor. When a wire/conductor carrying an electric current is placed above a magnetic needle, the needle will deflect clockwise or anticlockwise depending upon the direction of the current. If the current is in the same direction as the magnetic field, the needle will deflect clockwise. On the other hand, if the needle is in opposite direction to the magnetic field, the needle will deflect anticlockwise.

Key Concepts in Electromagnetism

1. Electric Field ($\mathbf{E}$): A region around a charged particle where electric forces can be felt by other charges. The electric field is measured in volts per meter (V/m) and is represented by the equation:

   $$\mathbf{E} = \frac{\mathbf{F}}{q}$$

   Where $\mathbf{F}$ is the force experienced by the charge, and $q$ is the magnitude of the charge.

2. Magnetic Field ($\mathbf{B}$): A field produced by moving electric charges and magnetic dipoles, which exerts a force on other moving charges and magnetic dipoles. The magnetic field is measured in teslas (T) and is represented by the Biot-Savart Law:

   $$\mathbf{B} = \frac{\mu_0}{4\pi} \int \frac{I \, d\mathbf{l} \times \mathbf{r}}{r^3}$$

   Where $\mu_0$ is the permeability of free space, $I$ is the current, $d\mathbf{l}$ is the differential length vector, and $\mathbf{r}$ is the position vector.

3. Electromagnetic Force: The force exerted by electric and magnetic fields on charged particles. This force can be calculated using the Lorentz force equation:

   $$\mathbf{F}=q(\mathbf{E}+\mathbf{v}\times \mathbf{B})$$

   Where $\mathbf{v}$ is the velocity of the charged particle.

4. Electromagnetic Waves: Oscillating electric and magnetic fields that propagate through space at the speed of light. Electromagnetic waves include visible light, radio waves, microwaves, and X-rays.

Maxwell's Equations

Maxwell's Equations are the cornerstone of electromagnetism, describing how electric and magnetic fields interact. These four equations are:

1. Gauss's Law for Electricity:

   $$\nabla \cdot \mathbf{E} = \frac{\rho}{\varepsilon_0}$$

   This equation describes how electric charges produce electric fields. 

2. Gauss's Law for Magnetism:

   $$\nabla \cdot \mathbf{B} = 0$$
   

   This law states that there are no magnetic monopoles; magnetic field lines are closed loops. 

3. Faraday's Law of Induction:

   $$\nabla \times \mathbf{E} = -\frac{\partial \mathbf{B}}{\partial t}$$

   Faraday's Law explains how changing magnetic fields induce electric currents. More information is available at Wikipedia.

4. Ampere-Maxwell Law:

   $$\nabla \times \mathbf{B} = \mu_0 \mathbf{J} + \mu_0 \varepsilon_0 \frac{\partial \mathbf{E}}{\partial t}$$

   This law connects magnetic fields to electric currents and changing electric fields. For further reading, visit Khan Academy.

Importance of Maxwell's Equations

Maxwell's Equations provide the foundation for understanding electromagnetic phenomena and have led to numerous technological advancements, including radio, television, and radar.

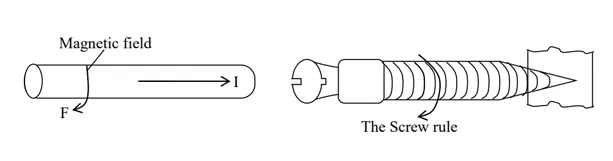
Relationship between the direction of current flow and the magnetic field

1) Corkscrew/Screw Rule

In order that the screw may travel in the same direction as the current, it has to be turned in the direction of the current (clockwise when viewed from the left – hand side) 

2) Grip Rule: 

The conductor is gripped with the right hand, with the thumb parallel to the conductor and pointing in the direction of the current. The fingers then points in the direction of the magnetic flux around the conductor.

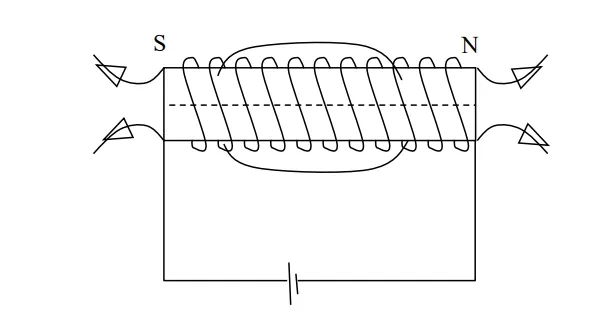
Magnetic Field of a Solenoid

A solenoid is a long coil of wire tightly wound in the shape of a helix. When an electric current flows through the solenoid, it produces a magnetic field similar to that of a bar magnet. This property makes solenoids essential components in various electromagnetic devices and applications.

Understanding the Magnetic Field in a Solenoid

The magnetic field generated by a solenoid is strong and uniform inside the coil, while it is much weaker and non-uniform outside the coil. This is because the turns of the wire are closely spaced, allowing their magnetic fields to add up constructively inside the solenoid. Outside the solenoid, the fields cancel each other out.

Characteristics of the Magnetic Field Inside a Solenoid

• Uniformity: The magnetic field inside an ideal solenoid is uniform, meaning that it has the same magnitude and direction at every point within the coil.
• Direction: The magnetic field lines inside a solenoid run parallel to the axis of the coil, from the south to the north end, forming closed loops as they exit and re-enter the solenoid.
• Magnitude: The strength of the magnetic field depends on the current flowing through the solenoid and the number of turns per unit length.

Formula for the Magnetic Field of a Solenoid

The magnetic field inside an ideal solenoid can be calculated using the formula:

$$B={\mu }_0\cdot n\cdot I$$

Where:

• $B$ is the magnetic field inside the solenoid (in teslas, T).
• $\mu_0$ is the permeability of free space ($4\pi \times 10^{-7} \, \text{T}\cdot\text{m/A}$).
• $n$ is the number of turns per unit length (in turns per meter, m$^{-1}$).
• $I$ is the current flowing through the solenoid (in amperes, A).

Derivation of the Formula

To derive this formula, consider Ampere’s Law, which states:

$$\oint \mathbf{B} \cdot d\mathbf{l} = \mu_0 \cdot I_{\text{enc}}$$

For a solenoid, the magnetic field $\mathbf{B}$ is constant inside and parallel to the solenoid, so the line integral simplifies to:

$$B \cdot L = \mu_0 \cdot n \cdot I \cdot L$$

Where $L$ is the length of the solenoid. Therefore, the magnetic field $B$ is given by:

$$B={\mu }_0\cdot n\cdot I$$

This derivation assumes an ideal solenoid, which means the solenoid is infinitely long and the effects at the ends are negligible.

Factors Affecting the Magnetic Field

1. Current ($I$): The magnetic field is directly proportional to the current flowing through the solenoid. Increasing the current will increase the magnetic field strength.

2. Number of Turns per Unit Length ($n$): The magnetic field is also directly proportional to the number of turns per unit length. More coils mean a stronger magnetic field.

3. Core Material: Introducing a ferromagnetic core, like iron, inside the solenoid significantly enhances the magnetic field due to the core’s high permeability compared to air.

Magnetic Field Outside a Solenoid

The magnetic field outside an ideal solenoid is approximately zero. This occurs because the external field lines are nearly parallel and cancel each other due to the solenoid’s symmetrical shape.

In practical solenoids, the magnetic field outside is weak but not zero, as the coil has finite length. However, for most applications, this external field can be considered negligible.

Practical Applications of Solenoids

Solenoids are widely used in various fields and devices due to their ability to convert electrical energy into mechanical motion and vice versa. Here are some common applications:

1. Electromagnets: Solenoids serve as the core component of electromagnets, providing a controllable and adjustable magnetic field for various uses, such as lifting heavy ferromagnetic objects.

2. Actuators: Solenoids are employed as actuators in electric locks, doorbells, and automotive starter motors. They convert electrical signals into linear motion to perform mechanical tasks.

3. Relays and Switches: In relays, solenoids are used to switch electrical circuits on and off, enabling control over large power loads with small input signals.

4. Magnetic Resonance Imaging (MRI): Solenoids are integral to MRI machines, where they generate strong magnetic fields necessary for producing detailed images of internal body structures.

5. Particle Accelerators: Solenoids are used in particle accelerators to direct and focus charged particles along a desired path.

Advanced Solenoid Concepts

In advanced studies, solenoids can be analyzed in various configurations, such as:

• Helmholtz Coils: Two solenoids aligned along the same axis to produce a uniform magnetic field in the region between them.

• Toroidal Solenoids: A solenoid bent into a circular shape, creating a magnetic field confined within the torus, minimizing external effects.

Experimenting with Solenoids

For those interested in hands-on learning, conducting experiments with solenoids can provide valuable insights into electromagnetic principles. Here are some simple experiments to try:

Experiment 1: Visualizing the Magnetic Field

Materials:

• Solenoid coil
• DC power supply
• Compass or iron filings
• Ferromagnetic core (optional)

Procedure:

1. Connect the solenoid to a DC power supply.
2. Use a compass to trace the magnetic field lines inside and outside the solenoid.
3. Alternatively, sprinkle iron filings around the solenoid and gently tap the surface to reveal the field pattern.
4. Observe how introducing a ferromagnetic core alters the magnetic field strength.

Experiment 2: Investigating Factors Affecting the Magnetic Field

Materials:

• Solenoid coil with variable turns
• DC power supply
• Ammeter
• Ferromagnetic core
• Ruler

Procedure:

1. Measure the solenoid's magnetic field strength using a sensor or compass.
2. Vary the current through the solenoid and observe the changes in field strength.
3. Alter the number of turns per unit length by adjusting the solenoid coil and record the effects.
4. Insert different core materials and note their impact on the magnetic field.

Determination of the north and south poles of a solenoid

The solenoid has north polarity at the end where the magnetic lines of flux leave and a south polarity flux enter (return). The polarity depends on the direction of current flow and the direction of winding.

 

FORCE DETERMINATION

Force on a Current-Carrying Conductor in a Magnetic Field

When an electric current flows through a conductor placed in a magnetic field, it experiences a force. This force is perpendicular to both the direction of the current and the magnetic field. The interaction between the current and the magnetic field is governed by the Lorentz force law.

Lorentz Force Law

The force ($\mathbf{F}$) on a current-carrying conductor in a magnetic field can be calculated using the following formula:

$$\mathbf{F}=I\mathbf{L}\times \mathbf{B}$$

Where:

• $\mathbf{F}$ is the magnetic force (in newtons, N).
• $I$ is the current flowing through the conductor (in amperes, A).
• $\mathbf{L}$ is the length vector of the conductor in the magnetic field (in meters, m), oriented in the direction of the current.
• $\mathbf{B}$ is the magnetic field vector (in teslas, T).

Understanding the Formula

• Direction of the Force: The direction of the force is given by the right-hand rule. Point the fingers of your right hand in the direction of the current ($\mathbf{L}$), curl them toward the magnetic field ($\mathbf{B}$), and your thumb will point in the direction of the force ($\mathbf{F}$).

• Magnitude of the Force: The magnitude of the force can be computed as:

$$F=I\cdot L\cdot B\cdot \sin (\theta )$$

Where $\theta$ is the angle between the current direction and the magnetic field. If the current is perpendicular to the magnetic field, $\sin(\theta)$ equals 1, and the formula simplifies to:

$$F=I\cdot L\cdot B$$

Example Calculation

Given:

• Current ($I$): 5 A
• Length of the conductor ($L$): 0.2 m
• Magnetic field ($B$): 0.3 T
• Angle ($\theta$): 90° (current is perpendicular to the magnetic field)

Calculation:

$$F = I \cdot L \cdot B \cdot \sin(\theta)$$
$$F = 5 \, \text{A} \cdot 0.2 \, \text{m} \cdot 0.3 \, \text{T} \cdot \sin(90^\circ)$$
$$F = 5 \cdot 0.2 \cdot 0.3 \cdot 1$$
$$F=0.3\text{N}$$

The force exerted on the conductor is 0.3 N.

Applications of the Lorentz Force

1. Electric Motors: The Lorentz force is utilized in electric motors to produce rotational motion. Current-carrying coils in a magnetic field experience forces that cause them to rotate, converting electrical energy into mechanical work.

2. Generators: In electrical generators, mechanical motion is converted into electrical energy using the Lorentz force. Conductors moving through a magnetic field induce an electromotive force (EMF) and generate current.

3. Magnetic Levitation: Magnetic levitation systems use the Lorentz force to counteract gravity, allowing objects to float above a magnetic surface. This principle is used in maglev trains and certain experimental setups.

4. Force Measurement: Devices like the galvanometer use the Lorentz force to measure current. The deflection of a current-carrying coil in a magnetic field is proportional to the amount of current, providing a means of measuring electrical flow.

For more information on electromagnetism and the Lorentz force, consider exploring the following resources:

• HyperPhysics: Lorentz Force
• Khan Academy: Magnetic Forces on Current-Carrying Wires
• Physics LibreTexts: Lorentz Force

Practical Considerations

• Uniform Magnetic Field: For accurate force calculations, the magnetic field should be uniform across the length of the conductor. Non-uniform fields can result in varying force distributions.

• Conductor Orientation: The angle between the conductor and the magnetic field affects the force magnitude. Optimal orientation is crucial for applications requiring maximum force.

• Field Strength: Increasing the magnetic field strength or the current will increase the force experienced by the conductor. This principle is utilized in designing electromagnetic devices to achieve desired performance levels

 

Numerical Examples

Problem 1:  A conductor carries a current of 800A at right angle to a magnetic field having a density of 0.5T and Length of 1 m

. Calculate the force on the conductor.

Given:

• Current ($I$) = 800 A
• Magnetic field ($B$) = 0.5 T
• Length ($L$) = 1 m
• The current is at a right angle to the magnetic field, so $\sin(90^\circ) = 1$

Calculation

To calculate the force on a conductor carrying a current in a magnetic field, we can use the formula:

$$F=B\cdot I\cdot L\cdot \sin (\theta )$$

where:

• $F$ is the force on the conductor (in newtons, N),
• $B$ is the magnetic flux density (in teslas, T),
• $I$ is the current through the conductor (in amperes, A),
• $L$ is the length of the conductor in the magnetic field (in meters, m),
• $\mathrm{\theta \; is\; the\; angle\; between\; the\; direction\; of\; the\; current\; and\; the\; magnetic\; field\; (in\; degrees\; or\; radians).}$

Given:

• Magnetic Flux Density ($B$): $0.5 \, \text{T}$
  
• Current ($I$): $800 \, \text{A}$
• Length of Conductor ($L$): $1 \, \text{m}$
• Angle ($\theta$): $90^{\circ \; (right\; angle)}$

Since the conductor is at right angles to the magnetic field, $\sin(90^\circ) = 1$.

Calculation:

$$F = B \cdot I \cdot L \cdot \sin(90^\circ)$$
$$F = 0.5 \, \text{T} \cdot 800 \, \text{A} \cdot 1 \, \text{m} \cdot 1$$
$$F = 400 \, \text{N}$$

Thus, the force on the conductor is 400 newtons.

Problem 2:    A conductor whose active length in a magnetic field is 0.5m carries a current 100A. If the flux density is 0.4T, calculate the force acting on the conductor.

Solution

To calculate the force acting on a conductor placed in a magnetic field, we use the formula for the magnetic force on a current-carrying conductor:

$$F=B\cdot I\cdot L\cdot \sin (\theta )$$

where:

• $F$ is the force on the conductor (in newtons, N),
• $B$ is the magnetic flux density (in teslas, T),
• $I$ is the current through the conductor (in amperes, A),
• $L$ is the length of the conductor in the magnetic field (in meters, m),
• $\theta$ is the angle between the direction of the current and the magnetic field (in degrees or radians).

Given:

• Magnetic Flux Density ($B$): $0.4 \, \text{T}$
  
• Current ($I$): $100 \, \text{A}$
• Length of Conductor ($L$): $0.5\text{m}$
• Angle ($\theta$): $90^{\circ \; (right\; angle,\; so }$$\sin(90^\circ) = 1$

Since the conductor is at right angles to the magnetic field, we use $\sin(90^\circ) = 1$.

Calculation:

$$F = B \cdot I \cdot L \cdot \sin(90^\circ)$$
$$F = 0.4 \, \text{T} \cdot 100 \, \text{A} \cdot 0.5 \, \text{m} \cdot 1$$
$$F = 0.4 \times 100 \times 0.5$$
$$F = 20 \, \text{N}$$

Thus, the force acting on the conductor is 20 newtons.

Problem 3: A conductor 0.3m long is carrying a current of 60A at right angle to the magnetic field. The force on the conductor is 8N. Calculate the flux density of the magnetic field.

Solution

To calculate the magnetic flux density ($B$) of the magnetic field, we can use the formula for the magnetic force on a current-carrying conductor:

$$F=B\cdot I\cdot L\cdot \sin (\theta )$$

where:

• $F$ is the force on the conductor (in newtons, N),
• $B$ is the magnetic flux density (in teslas, T),
• $I$ is the current through the conductor (in amperes, A),
• $L$ is the length of the conductor in the magnetic field (in meters, m),
• $\theta$ is the angle between the direction of the current and the magnetic field (in degrees or radians).

Given:

• Force ($F$): $8 \, \text{N}$
• Current ($I$): $60 \, \text{A}$
• Length of Conductor ($L$): $0.3 \, \text{m}$
• Angle ($\theta$): $90^\circ$ (right angle, so $\sin(90^\circ) = 1$

Since the conductor is at right angles to the magnetic field, we use $\sin(90^\circ) = 1$.

Formula Rearrangement:

To find the magnetic flux density $B$, rearrange the formula as follows:

$$B=\frac{F}{I\cdot L\cdot \sin (\theta )}$$

Calculation:

Substitute the given values into the formula:

$$B = \frac{8 \, \text{N}}{60 \, \text{A} \cdot 0.3 \, \text{m} \cdot 1}$$ $$B = \frac{8}{60 \times 0.3}$$ $$B = \frac{8}{18}$$ $$B = 0.4444 \, \text{T}$$

Therefore, the magnetic flux density of the magnetic field is approximately 0.44 T (Tesla).

Try Work

1.  A current – carrying conductor is situated at right angles to a uniform magnetic field having a density of 0.3T. calculate the force in Newton’s per meter length on the conductor when the current is 200A

2.  A conductor, 150mm long is carrying a current of 60A at right angles to a magnetic field the force on the conductor is 3N. Calculate the density of the field.

3. A straight conductor carries a current of 5A perpendicular to a magnetic field of flux density 1.2T. If the force acting on the conductor is 2N, calculate the effective length of the conductor in a magnetic field.

Induced EMF Due to Motion

When a conductor moves through a magnetic field, an electromotive force (EMF) is induced in the conductor. This phenomenon is explained by Faraday's Law of Electromagnetic Induction and is a key principle in electromagnetic systems such as generators and transformers.

Faraday’s Law of Induction

Faraday’s Law states that the induced EMF in a conductor is proportional to the rate of change of magnetic flux through the conductor. Mathematically, it can be expressed as:

$$\mathcal{E} = -\frac{d\Phi}{dt}$$

where $\mathcal{E}$ is the induced EMF, and $\Phi$ is the magnetic flux.

General Formula for Induced EMF

The formula for the induced EMF ($\mathcal{E}$) when a conductor moves through a magnetic field at an angle is:

$$\mathcal{E}=B\cdot v\cdot L\cdot \sin (\theta )$$

where:

• $B$ is the magnetic flux density (in teslas, T),
• $v$ is the velocity of the conductor (in meters per second, m/s),
• $L$ is the length of the conductor within the magnetic field (in meters, m),
• $\theta$ is the angle between the direction of the conductor’s motion and the direction of the magnetic field.

Explanation

• When $\theta = 90^\circ$: The motion is perpendicular to the magnetic field, and $\sin(\theta) = 1$. This gives the maximum induced EMF:

  $$\mathcal{E}=B\cdot v\cdot L$$

• When $\theta = 0^\circ$: The motion is parallel to the magnetic field, and $\sin(\theta) = 0$. In this case, the induced EMF is zero because there is no change in the magnetic flux through the conductor.

• For angles between 0° and 90°: The induced EMF is proportional to $\sin(\theta)$, reflecting the component of the motion that is perpendicular to the magnetic field.

Examples

Problem 1:. If a rod of length 0.5 m moves with a velocity of 2 m/s through a magnetic field of 0.3 T at an angle of 30° to the field:

$$\mathcal{E} = B \cdot v \cdot L \cdot \sin(\theta)$$
$$\mathcal{E} = 0.3 \, \text{T} \cdot 2 \, \text{m/s} \cdot 0.5 \, \text{m} \cdot \sin(30^\circ)$$
$$\mathcal{E} = 0.3 \cdot 2 \cdot 0.5 \cdot 0.5$$
$$\mathcal{E} = 0.15 \, \text{V}$$

So, the induced EMF would be 0.15 volts.

 

Problem 2: A conductor of active length 0.3m moves in a magnetic field at a linear velocity of 500ms^-1. If the magnetic flux density is 0.05T, calculate the value of the induced emf if the direction of movement of the conductor is 

a. Parallel to the field

b.      Perpendicular to the field

c.       At 30^o to the direction of the field.

 

Solution

To calculate the induced EMF in different scenarios, we use the formula:

$$\mathcal{E}=B\cdot v\cdot L\cdot \sin (\theta )$$

where:

• $\mathcal{E}$ is the induced EMF (in volts, V),
• $B$ is the magnetic flux density (in teslas, T),
• $v$ is the linear velocity of the conductor (in meters per second, m/s),
• $L$ is the length of the conductor within the magnetic field (in meters, m),
• $\theta$ is the angle between the direction of motion and the magnetic field.

Given:

• Length of the conductor ($\mathrm{L)\; =\; 0.3\; m}$
• Velocity ($v$) = 500 m/s
• Magnetic flux density ($B$) = 0.05 T

a. Parallel to the Field 

When the direction of movement is parallel to the magnetic field, $\sin(0^\circ) = 0$

$$\mathcal{E} = B \cdot v \cdot L \cdot \sin(0^\circ)$$
$$\mathcal{E} = 0.05 \, \text{T} \cdot 500 \, \text{m/s} \cdot 0.3 \, \text{m} \cdot 0$$
$$\mathcal{E} = 0 \, \text{V}$$

b. Perpendicular to the Field 

When the direction of movement is perpendicular to the magnetic field, $\sin(90^\circ) = 1$

$$\mathcal{E} = B \cdot v \cdot L \cdot \sin(90^\circ)$$
$$\mathcal{E} = 0.05 \, \text{T} \cdot 500 \, \text{m/s} \cdot 0.3 \, \text{m} \cdot 1$$
$$\mathcal{E} = 0.05 \cdot 500 \cdot 0.3$$
$$\mathcal{E} = 7.5 \, \text{V}$$

c. At 30° to the Direction of the Field 

When the direction of movement is at 30° to the magnetic field, $\sin (30^{\circ })=\mathrm{0.5\; .}$

$$\mathcal{E} = B \cdot v \cdot L \cdot \sin(30^\circ)$$
$$\mathcal{E} = 0.05 \, \text{T} \cdot 500 \, \text{m/s} \cdot 0.3 \, \text{m} \cdot 0.5$$
$$\mathcal{E} = 0.05 \cdot 500 \cdot 0.3 \cdot 0.5$$
$$\mathcal{E} = 3.75 \, \text{V}$$

Summary:

• Parallel to the field: $\mathcal{E}=0\text{V}$
• Perpendicular to the field: $\mathcal{E} = 7.5 \, \text{V}$
• At 30° to the field: $\mathcal{E} = 3.75 \, \text{V}$
  

Problem 3:  A coil of active length 300mm rotates in a uniform magnetic field between the poles of an electromagnetic, which gives a field of flux density, 0.02T. if the conductor speed is 12.6m/s, determine

a.       The maximum emf generated

b.      The emf generated when the conductor is at 60^o to the direction of the field.

 

Solution

Given Data:

• Active length of the coil ($L$) = 300 mm = 0.3 m
• Magnetic flux density ($B$) = 0.02 T
• Speed of the conductor ($v$) = 12.6 m/s
• The angle between the direction of the conductor and the magnetic field is 60° for one of the calculations.

a. Maximum EMF Generated

The maximum EMF occurs when the conductor is moving perpendicular to the magnetic field, meaning the angle ($\theta$) is 90°. The formula to find the induced EMF is:

$${\mathcal{E}}_{\text{max}}=B\cdot v\cdot L$$

Substitute the given values:

$$\mathcal{E}_{\text{max}} = 0.02 \, \text{T} \cdot 12.6 \, \text{m/s} \cdot 0.3 \, \text{m}$$
$$\mathcal{E}_{\text{max}} = 0.02 \cdot 12.6 \cdot 0.3$$
$$\mathcal{E}_{\text{max}} = 0.07572 \, \text{V}$$

So, the maximum EMF generated is approximately 0.0757 V (or 75.7 mV).

b. EMF Generated When the Conductor is at 60° to the Direction of the Field

When the conductor is at an angle of 60° to the magnetic field, the EMF is given by:

$$\mathcal{E}=B\cdot v\cdot L\cdot \sin (\theta )$$

where $\theta = 60^\circ$ and $\sin (60^{\circ })=\frac{\sqrt{3}}{2}\approx \mathrm{0.866 }$

Substitute the values:

$$\mathcal{E} = 0.02 \, \text{T} \cdot 12.6 \, \text{m/s} \cdot 0.3 \, \text{m} \cdot \sin(60^\circ)$$
$$\mathcal{E} = 0.02 \cdot 12.6 \cdot 0.3 \cdot 0.866$$
$$\mathcal{E} = 0.07572 \cdot 0.866$$
$$\mathcal{E} \approx 0.0656 \, \text{V}$$

So, the EMF generated when the conductor is at 60° to the direction of the field is approximately 0.0656 V (or 65.6 mV).

Direction of Induced EMF

The direction of induced electromotive force (EMF) is a fundamental concept in electromagnetism and electrical engineering. It describes how and why a voltage is generated in a conductor when it experiences a change in the magnetic field around it. This phenomenon is governed by Faraday's Law of Induction and Lenz's Law, which are crucial for the design and operation of various electrical devices.

Faraday's Law of Induction

Faraday's Law states that the induced EMF in a closed loop is directly proportional to the rate of change of the magnetic flux through the loop. Mathematically, it is expressed as:

$$\mathcal{E}=-\frac{d\mathrm{\Phi }}{d\mathrm{t}}$$

where:

• $\mathcal{E}$ is the induced EMF (in volts, V),
• $\Phi$ is the magnetic flux (in Weber, Wb),
• $\frac{d\Phi}{dt}$ represents the rate of change of magnetic flux.

Lenz's Law

Lenz's Law provides insight into the direction of the induced EMF. It states that the direction of the induced EMF is such that it opposes the change in magnetic flux that produced it. This law is a manifestation of the conservation of energy and ensures that the induced current will generate a magnetic field that counteracts the change in the external magnetic field.

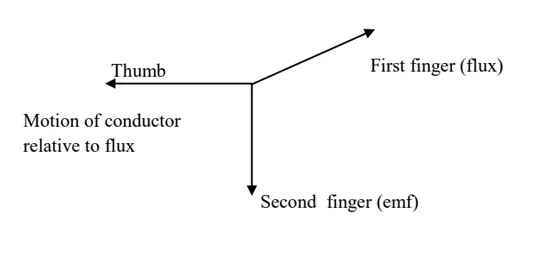
Determining the Direction of Induced EMF

To determine the direction of the induced EMF, you can use the following approaches:

• Right-Hand Rule: For a conductor moving through a magnetic field, point the thumb of your right hand in the direction of the motion and the fingers in the direction of the magnetic field. The direction in which your palm pushes (or the force you feel) indicates the direction of the induced current and thus the EMF.

• Lenz's Law Application: If the magnetic field is increasing, the induced current will flow in a direction that creates a magnetic field opposing the increase. Conversely, if the magnetic field is decreasing, the induced current will flow in a direction that creates a magnetic field that opposes the decrease.

Practical Applications

Understanding the direction of induced EMF is crucial for designing and troubleshooting electrical systems. It plays a vital role in:

• Electric Generators: Where mechanical energy is converted into electrical energy.
• Transformers: Which transfer electrical energy between circuits through electromagnetic induction.
• Induction Motors: Where the direction of the induced EMF affects motor rotation and efficiency.

Learn More

For a deeper understanding of how the direction of induced EMF affects various electrical devices and systems, you can explore this comprehensive resource on electromagnetic induction. It covers the theoretical foundations and practical applications in detail.

The laws of Electromagnetic Induction

Electromagnetic induction is a fundamental principle in electromagnetism that describes how electric current can be generated in a conductor by changing the magnetic field around it. The laws governing this phenomenon are crucial for understanding the operation of various electrical devices, such as generators, transformers, and inductors. The two primary laws of electromagnetic induction are Faraday's Law and Lenz's Law.

1. Faraday's Law of Electromagnetic Induction

Faraday's Law states that the electromotive force (EMF) induced in a circuit is directly proportional to the rate of change of the magnetic flux through the circuit. It is formulated as:

$$\mathcal{E}=-\frac{d\mathrm{\Phi }}{d\mathrm{t}}$$

where:

• $\mathcal{E}$ is the induced EMF (in volts, V),
• $\Phi$ is the magnetic flux (in Weber, Wb),
• $\frac{d\Phi}{dt}$ represents the rate of change of magnetic flux.

Key Points:

• Magnitude of Induced EMF: The greater the rate at which the magnetic flux changes, the larger the induced EMF. This can occur by changing the strength of the magnetic field, moving the conductor through the field, or altering the area of the conductor loop in the field.

• Magnetic Flux: Magnetic flux ($\Phi$) is the product of the magnetic field strength ($B$), the area of the conductor loop ($A$), and the cosine of the angle ($\theta$) between the magnetic field and the normal to the surface of the loop. Mathematically, it is expressed as:

$$\Phi = B \cdot A \cdot \cos(\theta)$$

2. Lenz's Law

Lenz's Law provides the direction of the induced EMF and current. It states that the direction of the induced current is such that it creates a magnetic field opposing the change in the original magnetic flux that caused it. Mathematically, it is incorporated into Faraday's Law by the negative sign:

$$\mathcal{E}=-\frac{d\mathrm{\Phi }}{d\mathrm{t}}$$

Key Points:

• Opposition to Change: Lenz's Law reflects the conservation of energy principle. The induced current generates its own magnetic field that opposes the change in the external magnetic field. For example, if the magnetic field through a loop is increasing, the induced current will generate a field that opposes this increase.

• Induced EMF Direction: The negative sign in Faraday's Law signifies that the induced EMF and resulting current will act in a direction to counteract the change in magnetic flux.

Practical Applications

Understanding these laws is essential for the design and functioning of various electromagnetic devices:

• Electric Generators: Convert mechanical energy into electrical energy using the principles of Faraday's Law.
• Transformers: Use electromagnetic induction to transfer electrical energy between circuits.
• Inductors: Utilize electromagnetic induction to store energy in a magnetic field.

Further Reading

To explore these concepts in more detail and see their applications in various electrical and electronic systems, you can visit Electromagnetic Induction: Basics and Applications. This resource provides a comprehensive overview of electromagnetic induction principles and their practical uses.

 

Numerical Example

Problem 1:. A magnetic flux 400µWb passing through a coil of 1200 turns is reversed in 0.1s. Calculate the average value of the emf induced in the coil.

 

Solution

The formula to find the average EMF induced is:

$${\mathcal{E}}_{\text{avg}}=-\frac{N\cdot \mathrm{\Delta }\mathrm{\Phi }}{\mathrm{\Delta }\mathrm{t}}$$

where:

• $\mathcal{E}_{\text{avg}}$ is the average induced EMF,
• $N$ is the number of turns in the coil,
• $\Delta \Phi$ is the change in magnetic flux,
• $\Delta t$ is the time over which the change occurs.

Given Data

• Initial Magnetic Flux ($\Phi_{\text{initial}}$): $400 \, \mu\text{Wb} = 400 \times 10^{-6} \, \text{Wb} = 0.0004 \, \text{Wb}$
• Final Magnetic Flux ($\Phi_{\text{final}}$): Since the flux is reversed, it will be $-400 \, \mu\text{Wb} = -0.0004 \, \text{Wb}$
• Number of Turns ($N$): 1200
• Time Interval ($\Delta t$): $0.1 \, \text{s}$

Calculation

Change in Magnetic Flux ($\mathrm{\Delta }$$\mathrm{\Phi }$)

The change in magnetic flux when it is reversed is given by:

$$\Delta \Phi = \Phi_{\text{final}} - \Phi_{\text{initial}}$$ $$\Delta \Phi = (-0.0004 \, \text{Wb}) - (0.0004 \, \text{Wb})$$
$$\Delta \Phi = -0.0008 \, \text{Wb}$$

The total change in flux is $0.0008 \, \text{Wb}$ (as a magnitude, ignoring the negative sign for calculation).

Average Induced EMF ($\mathcal{E}$)

Now, substitute the values into Faraday's Law:

$$\mathcal{E} = -N \cdot \frac{\Delta \Phi}{\Delta t}$$ $$\mathcal{E} = -1200 \cdot \frac{-0.0008 \, \text{Wb}}{0.1 \, \text{s}}$$ $$\mathcal{E} = 1200 \cdot \frac{0.0008}{0.1}$$ $$\mathcal{E} = 1200 \cdot 0.008$$
$$\mathcal{E} = 9.6 \, \text{V}$$

Result

The average EMF induced in the coil is 9.6 volts.

Problem 2:. A magnetic flux 2mWb links with a coil of 100turns. If the flux

a)      Doubled

b)      Reversed in a time of 20ms. Calculate the value of the emf induced in the coil.

 

Solution

The formula for the induced EMF ($\mathcal{E}$) is:

$$\mathcal{E} = -\frac{N \cdot \Delta \Phi}{\Delta t}$$

where:

• $N$ is the number of turns in the coil,
• $\Delta \Phi$ is the change in magnetic flux,
• $\Delta t$ is the time over which the change occurs.

Given:

• Initial magnetic flux, $\Phi_{\text{initial}}$ = 2 mWb = 2 × 10⁻³ Wb
• Number of turns, $N$ = 100
• Time interval, $\Delta t$ = 20 ms = 20 × 10⁻³ s

a) Flux Doubled

When the flux is doubled, the final flux $\Phi_{\text{final}}$ is:

$$\Phi_{\text{final}} = 2 \times \Phi_{\text{initial}}$$ $$\Phi_{\text{final}} = 2 \times 2 \times 10^{-3} \, \text{Wb}$$
$$\Phi_{\text{final}} = 4 \times 10^{-3} \, \text{Wb}$$

Change in Magnetic Flux ($\Delta \Phi$):

$$\Delta \Phi = \Phi_{\text{final}} - \Phi_{\text{initial}}$$ $$\Delta \Phi = 4 \times 10^{-3} - 2 \times 10^{-3}$$
$$\Delta \Phi = 2 \times 10^{-3} \, \text{Wb}$$

Calculate the EMF:

$$\mathcal{E} = -\frac{N \cdot \Delta \Phi}{\Delta t}$$ $$\mathcal{E} = -\frac{100 \cdot 2 \times 10^{-3}}{20 \times 10^{-3}}$$ $$\mathcal{E} = -\frac{0.2}{0.02}$$ $$\mathcal{E} = -10 \, \text{V}$$

The negative sign indicates the direction of the induced EMF, but the magnitude is 10 V.

b) Flux Reversed

When the flux is reversed, the final flux $\Phi_{\text{final}}$ is:

$$\Phi_{\text{final}} = -\Phi_{\text{initial}}$$ $$\Phi_{\text{final}} = -2 \times 10^{-3} \, \text{Wb}$$

Change in Magnetic Flux ($\Delta \Phi$):

$$\Delta \Phi = \Phi_{\text{final}} - \Phi_{\text{initial}}$$ $$\Delta \Phi = -2 \times 10^{-3} - 2 \times 10^{-3}$$
$$\Delta \Phi = -4 \times 10^{-3} \, \text{Wb}$$

Calculate the EMF:

$$\mathcal{E} = -\frac{N \cdot \Delta \Phi}{\Delta t}$$ $$\mathcal{E} = -\frac{100 \cdot (-4 \times 10^{-3})}{20 \times 10^{-3}}$$ $$\mathcal{E} = \frac{0.4}{0.02}$$ $$\mathcal{E} = 20 \, \text{V}$$

The positive value indicates the magnitude of the induced EMF, which is 20 V.

Summary:

• When the flux is doubled: The induced EMF is 10 V.
• When the flux is reversed: The induced EMF is 20 V.

 

Self-Inductance

A circuit is said to have self-inductance when a  change in its own current (by means of a variable resistor) cause a change in its magnetic flux thereby inducing emf into it.

The unit of self-inductance is Henry (H) 

Henry (H)

Henry (H) is the SI unit of inductance, named after the American scientist Joseph Henry. Inductance is a fundamental property of electrical circuits, particularly those involving coils or inductors, which measures the ability of a conductor to induce electromotive force (EMF) when the current flowing through it changes.

Definition of Henry

A circuit has an inductance of one Henry when a current change of one ampere per second induces an electromotive force of one volt across the conductor. Mathematically, the relationship is given by:

$$\mathcal{E}=-L\cdot \frac{dI}{dt}$$

where:

• $\mathcal{E}$ is the induced EMF (in volts, V),
• $L$ is the inductance (in Henrys, H),
• $\frac{dI}{dt}$ is the rate of change of current (in amperes per second, A/s).

Practical Examples

• Solenoid and Coils: Devices like transformers and inductors often have inductance measured in Henrys. A typical inductor might have a value of a few millihenrys (mH) or microhenrys (µH).
• Applications: Inductors are used in filters, oscillators, and tuning circuits, relying on the principles of inductance to control current and voltage.

Calculation of Inductance

Inductance ($L$) for a solenoid can be calculated using the formula:

$$L = \frac{N^2 \cdot \mu \cdot A}{l}$$

where:

• $N$ is the number of turns in the coil,
• $\mu$ is the magnetic permeability of the core material (in henry per meter, H/m),
• $A$ is the cross-sectional area of the coil (in square meters, m²),
• $l$ is the length of the coil (in meters, m).

Energy stored in a coil 

The energy stored in a coil (or inductor) is given by the formula:

$$E=\frac{1}{2}L{I}^2$$

where:

• $E$ is the energy stored in the coil (in joules, J),
• $L$ is the inductance of the coil (in henries, H),
• $I$ is the current flowing through the coil (in amperes, A).

Explanation

• Inductance ($L$): This measures the coil's ability to store energy in its magnetic field. A higher inductance means more energy can be stored for a given current.
• Current ($I$): The amount of current flowing through the coil affects the energy stored. The energy is proportional to the square of the current, meaning that doubling the current will increase the stored energy by a factor of four.

Derivation

The formula is derived from the work done to build up the current in the coil, taking into account the fact that the voltage across an inductor is proportional to the rate of change of current:

$$V=L\frac{dI}{d\mathrm{t}}$$

The infinitesimal amount of work $dW$ done to move a small amount of current $dI$ is:

$$dW = V \cdot dI$$

$$dW=L\frac{dI}{dt}\cdot dI$$

Rearrange and integrate with respect to $I$ from 0 to $I$:

$$W = \int_{0}^{I} L I \, dI$$
$$W = \frac{1}{2} L I^2$$

Numerical Examples

Problem 1: Calculate the average value of the emf induced in a coil of 0.4H inductance when in a time internal of 0.05seconds, the current 

a.       Increases from 0.1A to 2.1A

b.      Reduces from 0.5A to 0.05A

Solution

To calculate the average value of the EMF induced in a coil given its inductance and the change in current over a specific time interval, we use the formula for inductive EMF:

$$\mathcal{E} = -L \cdot \frac{\Delta I}{\Delta t}$$

where:

• $\mathcal{E}_{\text{avg}}$ is the average induced EMF (in volts, V),
• $L$ is the inductance of the coil (in henries, H),
• $\mathrm{\Delta }\mathrm{I\; is\; the\; change\; in\; current\; (in\; amperes,\; A),}$
• $\Delta t$ is the time interval over which the current changes (in seconds, s).

Given Data:

• Inductance, $L=0.4\text{H }$
• Time interval, $\Delta t = 0.05 \, \text{s}$
  

a) Current Increases from 0.1 A to 2.1 A

Change in Current ($\mathrm{\Delta }$$I$):

• Initial current, $I_{\text{initial}} = 0.1 \, \text{A}$
• Final current, $I_{\text{final}}=2.1\text{A }$

$$\Delta I = I_{\text{final}} - I_{\text{initial}}$$ $$\Delta I = 2.1 - 0.1$$
$$\Delta I = 2.0 \, \text{A}$$

Calculate the Average Induced EMF:

$$\mathcal{E}_{\text{avg}} = -L \cdot \frac{\Delta I}{\Delta t}$$ $$\mathcal{E}_{\text{avg}} = -0.4 \cdot \frac{2.0}{0.05}$$ $$\mathcal{E}_{\text{avg}} = -0.4 \cdot 40$$
$$\mathcal{E}_{\text{avg}} = -16 \, \text{V}$$

Thus, the average induced EMF when the current increases from 0.1 A to 2.1 A is 16 V (the negative sign indicates the direction of EMF opposing the change, but the magnitude is 16 V).

b) Current Reduces from 0.5 A to 0.05 A

Change in Current ($\Delta I$):

• Initial current, $I_{\text{initial}}=0.5\text{A }$
• Final current, $I_{\text{final}}=0.05\text{A }$

$$\Delta I = I_{\text{final}} - I_{\text{initial}}$$ $$\Delta I = 0.05 - 0.5$$
$$\Delta I = -0.45 \, \text{A}$$

Calculate the Average Induced EMF:

$$\mathcal{E}_{\text{avg}} = -L \cdot \frac{\Delta I}{\Delta t}$$ $$\mathcal{E}_{\text{avg}} = -0.4 \cdot \frac{-0.45}{0.05}$$ $$\mathcal{E}_{\text{avg}} = -0.4 \cdot (-9)$$
$$\mathcal{E}_{\text{avg}} = 3.6 \, \text{V}$$

Thus, the average induced EMF when the current reduces from 0.5 A to 0.05 A is 3.6 V.

Summary:

• When current increases from 0.1 A to 2.1 A: The induced EMF is 16 V.
• When current reduces from 0.5 A to 0.05 A: The induced EMF is 3.6 V.

Problem 2: A coil of 10turns produces a flux which changes from 0.5Wb to 2Wb and current 3A to 5A. Calculate the inductance of the coil.

Solution

To calculate the inductance of a coil, we need to consider the change in magnetic flux and the corresponding change in current. The formula for inductance $L$ based on these changes is derived from Faraday's Law and is given by:

$$L=\frac{N\cdot \mathrm{\Delta }\mathrm{\Phi }}{\mathrm{\Delta }\mathrm{I}}$$

where:

• $L$ is the inductance (in henries, H),
• $N$ is the number of turns in the coil,
• $\Delta \Phi$ is the change in magnetic flux (in webers, Wb),
• $\mathrm{\Delta }\mathrm{I\; is\; the\; change\; in\; current\; (in\; amperes,\; A).}$

Given Data:

• Number of turns, $N=\mathrm{10 }$
  
• Initial flux, $\Phi_{\text{initial}} = 0.5 \, \text{Wb}$
• Final flux, $\Phi_{\text{final}} = 2.0 \, \text{Wb}$
• Initial current, $I_{\text{initial}}=3.0\text{A }$
• Final current, $I_{\text{final}} = 5.0 \, \text{A}$
  

Step-by-Step Calculation

1. Calculate the Change in Magnetic Flux ($\mathrm{\Delta }$$\mathrm{\Phi }$):

$$\Delta \Phi = \Phi_{\text{final}} - \Phi_{\text{initial}}$$ $$\Delta \Phi = 2.0 \, \text{Wb} - 0.5 \, \text{Wb}$$
$$\Delta \Phi = 1.5 \, \text{Wb}$$

2. Calculate the Change in Current ($\mathrm{\Delta }$$I$):

$$\Delta I = I_{\text{final}} - I_{\text{initial}}$$ $$\Delta I = 5.0 \, \text{A} - 3.0 \, \text{A}$$
$$\Delta I = 2.0 \, \text{A}$$

3. Calculate the Inductance ($L$):

$$L = \frac{N \cdot \Delta \Phi}{\Delta I}$$ $$L = \frac{10 \cdot 1.5}{2.0}$$ $$L = \frac{15}{2.0}$$ $$L = 7.5 \, \text{H}$$

Result

The inductance of the coil is 7.5 henries (H).

Problem 3: A solenoid of self – inductance 5H carries a current of 2A. Determine the 

a.       Energy stored in the magnetic circuit if the current is reduced to 0.5A, determine the 

b.      New value of stored energy

c.       Energy released into the electrical circuit

Solution

The energy ($W$) stored in an inductor is given by:

$$W=\frac{1}{2}L{I}^2$$

where:

• $W$ is the energy stored in the inductor (in joules, J),
• $L$ is the self-inductance of the solenoid (in henries, H),
• $I$ is the current through the solenoid (in amperes, A).

Given:

• Self-inductance, $L=5\text{H }$
• Initial current, $I_{\text{initial}}=2\text{A }$
• Final current, $I_{\text{final}} = 0.5 \, \text{A}$

a. Energy Stored in the Magnetic Circuit with Initial Current

Using the initial current of 2A, we can calculate the initial energy stored:

$$W_{\text{initial}} = \frac{1}{2} \cdot L \cdot I_{\text{initial}}^2$$ $$W_{\text{initial}} = \frac{1}{2} \cdot 5 \cdot (2)^2$$
$$W_{\text{initial}} = \frac{1}{2} \cdot 5 \cdot 4$$
$$W_{\text{initial}} = \frac{1}{2} \cdot 20$$
$$W_{\text{initial}} = 10 \, \text{J}$$

Thus, the initial energy stored in the magnetic circuit is 10 joules.

b. New Value of Stored Energy with Reduced Current

Now, with the current reduced to 0.5A, we can calculate the new stored energy:

$$W_{\text{final}} = \frac{1}{2} \cdot L \cdot I_{\text{final}}^2$$ $$W_{\text{final}} = \frac{1}{2} \cdot 5 \cdot (0.5)^2$$
$$W_{\text{final}} = \frac{1}{2} \cdot 5 \cdot 0.25$$
$$W_{\text{final}} = \frac{1}{2} \cdot 1.25$$
$$W_{\text{final}} = 0.625 \, \text{J}$$

Thus, the new energy stored in the magnetic circuit is 0.625 joules.

c. Energy Released into the Electrical Circuit

The energy released into the electrical circuit as the current is reduced from 2A to 0.5A is the difference between the initial and final stored energies:

$$\Delta W = W_{\text{initial}} - W_{\text{final}}$$ $$\Delta W = 10 - 0.625$$
$$\Delta W = 9.375 \, \text{J}$$

Thus, the energy released into the electrical circuit is 9.375 joules.

Summary

• Initial Energy Stored: $10\text{J}$
• New Energy Stored: $0.625\text{J}$
• Energy Released: $9.375\text{J}$

This analysis shows that reducing the current from 2A to 0.5A significantly decreases the energy stored in the magnetic circuit and results in the release of 9.375 joules of energy into the electrical circuit.

Trial Test

Problem 1:.      A conductor of active length 0.5m moves in a magnetic field at a linear speed of 600ms^-1. If the magnetic flux density is 0.04J, calculate the value of the induced emf of the direction of movement of the conductor is 

a.       At 45^oto the direction of the field

b.      Parallel to the field

c.       Perpendicular to the field

Problem 2:.      State and explain two methods by which emf can be induced in a conductor.

Problem 3:.      State Faraday’s second law of electromagnetic induction

b. A magnetic flux of 300mWb passing through a coil of 1600turns is revered in 0.2sec.

Calculate the average value of the emf induced in the coil

Problem 4:.      A solenoid of self – inductance 6H carries a current of 3A. Determine the 

a.       Energy stored in the magnetic circuit If the current is reduced to 0.6A determine the; 

b.      New value of stored energy

c.       Energy released into the electrical circuit

Eddy Current Loss

Eddy current loss is due to circulating currents set up in the core (steel lamination) of a machine.

It can be reduced by

a)      Laminating the core

b)      Using silicon – iron alloy. (the resistivity of silicon alloy is higher than steel)

 

Mutual Inductance: A Comprehensive Overview

Mutual inductance is a fundamental concept in electromagnetism and electrical engineering, referring to the phenomenon where a change in current in one coil induces an electromotive force (EMF) in another nearby coil. This interaction is essential in many applications, including transformers, inductors, and various types of electrical circuits. In this article, we will explore the principles of mutual inductance, its mathematical representation, applications, and some real-world examples.

---

Understanding Mutual Inductance

Mutual inductance occurs when two or more coils are placed in close proximity, such that the magnetic field generated by the current flowing through one coil influences the other coil(s). The key point is that the magnetic field lines from one coil (primary coil) link with the turns of another coil (secondary coil), leading to induced EMF due to changes in current.

Fundamental Principle

The concept of mutual inductance is based on Faraday's Law of Electromagnetic Induction, which states that a changing magnetic field within a closed loop induces an EMF in that loop. The magnitude of the induced EMF in the secondary coil is proportional to the rate of change of current in the primary coil.

Formula for Mutual Inductance

The mutual inductance ($M$) between two coils can be defined by the formula::

$$\mathcal{E}_{\text{induced}} = -M \frac{dI_1}{dt}$$where:

• $\mathcal{E}_{\text{induced}}$ is the induced EMF in the secondary coil (in volts, V).
• $M$ is the mutual inductance between the coils (in henries, H).
• $\frac{dI_1}{dt}$ is the rate of change of current in the primary coil (in amperes per second, A/s).

The negative sign in the equation is a consequence of Lenz's Law, which indicates that the direction of the induced EMF opposes the change in current that produced it.

Calculation of Mutual Inductance

For two coils that are closely wound together, the mutual inductance can also be expressed as:

$$M=k\sqrt{L_1{L}_2}$$

where:

• $M$ is the mutual inductance (in henries, H).
• $k$ is the coupling coefficient (dimensionless), ranging from 0 to 1. It represents the effectiveness of the magnetic coupling between the coils.
• $L_1$ and $L_2$ are the self-inductances of the primary and secondary coils, respectively (in henries, H).

---

Applications of Mutual Inductance

Mutual inductance is utilized in a variety of electrical and electronic devices and systems. Here are some common applications:

1. Transformers

Transformers are devices that rely on mutual inductance to transfer electrical energy between two or more circuits. They consist of primary and secondary coils wrapped around a common core. The primary coil is connected to an AC power source, and the changing current induces an EMF in the secondary coil, effectively transforming the voltage level.

• Step-up Transformers: Increase the voltage from primary to secondary coil.
• Step-down Transformers: Decrease the voltage from primary to secondary coil.

For more details on transformers and their operation, refer to How Transformers Work.

2. Inductive Coupling

Inductive coupling is used in wireless power transfer, where energy is transmitted between coils without direct electrical contact. Applications include wireless chargers for smartphones and electric toothbrushes, as well as medical implants like pacemakers.

• Example: Wireless charging pads use inductive coupling to charge devices placed on them, utilizing mutual inductance principles.

3. Inductive Sensors

Inductive sensors exploit mutual inductance to detect changes in position, velocity, or presence of metallic objects. They are widely used in industrial automation for proximity sensing and other measurement tasks.

• Example: An inductive proximity sensor detects metal objects by inducing currents in them and analyzing the resultant magnetic field changes.

4. Signal Coupling in Communication Systems

In communication systems, mutual inductance is used for coupling signals between different stages of a circuit without direct electrical connections. Transformers provide impedance matching and isolation between circuits.

• Example: Audio transformers use mutual inductance to transmit audio signals between devices, such as amplifiers and speakers.

---

Examples and Calculations

Let's explore a few example problems to understand mutual inductance in practical scenarios.

Example 1: Calculating Mutual Inductance

Problem: Two coils have self-inductances of $L_1=4\text{H and }$$L_2 = 9 \, \text{H}$. The coupling coefficient between them is $k = 0.8$. Calculate the mutual inductance $M$.

Solution:

$$M = k \sqrt{L_1 L_2}$$ $$M = 0.8 \sqrt{4 \times 9}$$ $$M = 0.8 \times \sqrt{36}$$ $$M = 0.8 \times 6$$
$$M = 4.8 \, \text{H}$$

The mutual inductance between the coils is 4.8 henries.

Example 2: Induced EMF in a Coil

Problem: A primary coil with a mutual inductance of $3 \, \text{H}$ is experiencing a change in current from 2 A to 6 A over 0.5 seconds. Calculate the induced EMF in the secondary coil.

Solution:

First, calculate the rate of change of current:

$$\frac{dI_1}{dt} = \frac{I_{\text{final}} - I_{\text{initial}}}{\Delta t}$$ $$\frac{dI_1}{dt} = \frac{6 - 2}{0.5}$$ $$\frac{dI_1}{dt} = \frac{4}{0.5}$$ $$\frac{dI_1}{dt} = 8 \, \text{A/s}$$

Now, use the mutual inductance formula to find the induced EMF:

$$\mathcal{E}_{\text{induced}} = -M \frac{dI_1}{dt}$$ $$\mathcal{E}_{\text{induced}} = -3 \times 8$$
$$\mathcal{E}_{\text{induced}} = -24 \, \text{V}$$

The induced EMF in the secondary coil is 24 volts, with the negative sign indicating opposition to the change.

Problem: The mutual inductance between two coils is 0.15H. If the current in the primary winding increases from 0.2A to 0.5A in 10ms,

a.       Determine the average value of emf induced in the secondary winding during this period of time 

b.      If the secondary winding is 400turns, determine the change in the flux which mutually links the coil

Solution

To solve this problem, we need to determine the average electromotive force (EMF) induced in the secondary winding due to a change in current in the primary winding, and then find the change in magnetic flux linked with the secondary coil.

Given Data:

• Mutual Inductance: $M = 0.15 \, \text{H}$
• Initial Current: $I_{\text{initial}} = 0.2 \, \text{A}$
• Final Current: $I_{\text{final}}=0.5\text{A}$
• Time Interval: $\Delta t = 10 \, \text{ms} = 0.01 \, \text{s}$
• Turns in Secondary Winding: $N_2 = 400$

a. Determine the Average EMF Induced in the Secondary Winding

The formula for the EMF ($\mathcal{E}$) induced in the secondary winding due to a change in current in the primary winding is given by:

$${\mathcal{E}}_{\text{induced}}=-M\frac{\mathrm{\Delta }I}{\mathrm{\Delta }\mathrm{t}}$$

where:

• $\mathcal{E}_{\text{induced}}$ is the average induced EMF (in volts, V),
• $M$ is the mutual inductance (in henries, H),
• $\Delta I$ is the change in current (in amperes, A),
• $\Delta t$ is the change in time (in seconds, s).

Calculate the Change in Current ($\mathrm{\Delta }$$I$):

$$\Delta I = I_{\text{final}} - I_{\text{initial}}$$ $$\Delta I = 0.5 \, \text{A} - 0.2 \, \text{A}$$
$$\Delta I = 0.3 \, \text{A}$$

Calculate the Average Induced EMF:

$$\mathcal{E}_{\text{induced}} = -M \frac{\Delta I}{\Delta t}$$ $$\mathcal{E}_{\text{induced}} = -0.15 \, \text{H} \times \frac{0.3 \, \text{A}}{0.01 \, \text{s}}$$ $$\mathcal{E}_{\text{induced}} = -0.15 \times 30$$
$$\mathcal{E}_{\text{induced}} = -4.5 \, \text{V}$$

The average EMF induced in the secondary winding is 4.5 V. The negative sign indicates that the induced EMF opposes the change in current in the primary winding according to Lenz's Law.

b. Determine the Change in Flux Linked with the Secondary Coil

To find the change in magnetic flux ($\Delta \Phi$) that links the secondary winding, we can use the relationship between mutual inductance, change in current, and change in flux:

$$M=\frac{N_2\cdot \mathrm{\Delta }\mathrm{\Phi }}{\mathrm{\Delta }\mathrm{I}}$$

Rearranging the formula gives:

$$\Delta \Phi = \frac{M \cdot \Delta I}{N_2}$$

Calculate the Change in Flux ($\mathrm{\Delta }$$\mathrm{\Phi }$):

$$\Delta \Phi = \frac{0.15 \, \text{H} \times 0.3 \, \text{A}}{400}$$ $$\Delta \Phi = \frac{0.045}{400}$$ $$\Delta \Phi = 0.0001125 \, \text{Wb}$$
$$\Delta \Phi = 112.5 \, \mu\text{Wb}$$

The change in the flux that mutually links the secondary coil is 112.5 micro webers ($\mu\text{Wb}$).

Summary:

• Average Induced EMF: $4.5 \, \text{V}$
• Change in Flux: $112.5 \, \mu\text{Wb}$

---

Importance of Mutual Inductance

Mutual inductance is a cornerstone concept in modern electronics, enabling the design and operation of numerous devices and systems. It facilitates energy transfer, isolation, and coupling in electrical networks, making it a fundamental principle for engineers and scientists.

Further Reading

For more in-depth knowledge on mutual inductance, consider exploring these resources:

• HyperPhysics: Inductance
• Khan Academy: Mutual Inductance

Applications of Electromagnetism

Electromagnetism has a wide range of applications in various fields, from engineering to medicine. Here are some notable applications:

1. Electric Motors and Generators

Electric motors convert electrical energy into mechanical energy, while generators do the opposite. These devices are essential in powering industrial machinery, household appliances, and electric vehicles. The principle behind their operation is electromagnetic induction, where a changing magnetic field produces an electromotive force (EMF). To learn more about electric motors, visit Electronics Tutorials.

2. Communication Systems

Electromagnetic waves are used in communication systems to transmit information over long distances. Radio waves, microwaves, and infrared waves are commonly employed in wireless communication technologies, including cell phones, Wi-Fi, and satellite communication. Learn more about electromagnetic communication at RF Wireless World.

3. Medical Imaging

Techniques like Magnetic Resonance Imaging (MRI) and X-rays rely on electromagnetic principles to create detailed images of the human body. MRI uses strong magnetic fields and radio waves to visualize soft tissues, while X-rays utilize high-energy electromagnetic waves to examine bones and dense structures. For more information on MRI, visit RadiologyInfo.org.

4. Electromagnetic Levitation

Electromagnetic levitation, or maglev, is a technology that allows objects to float using magnetic fields. This principle is used in maglev trains, which operate without contact with the ground, reducing friction and allowing for high-speed transportation. Learn more about maglev trains at HowStuffWorks.

5. Inductive Charging

Inductive charging is a method of wirelessly charging devices using electromagnetic fields. This technology is widely used in charging electric toothbrushes, smartphones, and electric vehicles. It operates on the principle of electromagnetic induction, where an alternating magnetic field induces a current in a nearby conductor. For further reading on inductive charging, visit HowStuffWorks.

The Future of Electromagnetism

The future of electromagnetism promises exciting developments as researchers continue to explore new applications and technologies. Some emerging trends include:

1. Quantum Electrodynamics (QED)

Quantum Electrodynamics is a field that studies the interaction of light and matter at the quantum level. It seeks to explain electromagnetic phenomena with greater precision, providing insights into fundamental particles and forces. To learn more about QED, visit Physics LibreTexts.

2. Electromagnetic Cloaking

Electromagnetic cloaking aims to make objects invisible by bending electromagnetic waves around them. This technology has potential applications in stealth technology and telecommunications. Researchers are exploring metamaterials that can achieve this effect. For more information on electromagnetic cloaking, visit ScienceDirect.

3. Wireless Power Transmission

Wireless power transmission aims to deliver electricity over long distances without cables. This technology could revolutionize power distribution, reducing the need for extensive electrical grids. Researchers are investigating methods to transmit power efficiently using electromagnetic waves. To learn more about wireless power transmission, visit IEEE Xplore.

Conclusion

Electromagnetism is a profound and versatile field of science that has transformed our world. From everyday applications like electric motors and communication systems to cutting-edge technologies like quantum electrodynamics and electromagnetic cloaking, electromagnetism continues to be at the forefront of scientific and technological advancements.

By understanding the principles of electromagnetism and exploring its applications, we gain valuable insights into the forces that shape our universe. Whether you're a student, engineer, or enthusiast, there's always more to discover in this fascinating field.

For further exploration and educational resources, consider visiting the following sites:

• HyperPhysics: Comprehensive resource on electromagnetism concepts.
• Khan Academy: Interactive lessons on electromagnetic fields and forces.
• Physics LibreTexts: In-depth articles on electromagnetic theory and applications.
• Wikipedia - Electromagnetism: Overview and detailed information on electromagnetism and related topics.
• Electronics Tutorials: Tutorials on electric motors and electromagnetic devices.

Related Topics on Applied Electricity 

• Emission of Electrons and Thermionic Devices
• Data Communication 
• Digital Electronics
• Magnetic Field
• Electromagnetism
• Electric Field
• Direct Current Circuit Theory
• Applied Electricity Concise Notes for Senior High Schools (SHS 1, 2 & SHS 3)
• Careers in Applied Electricity
• Common Electrical Devices and Their Uses
• The Impact of Applied Electricity on Modern Technology